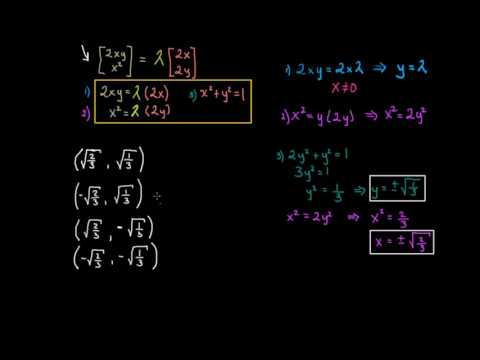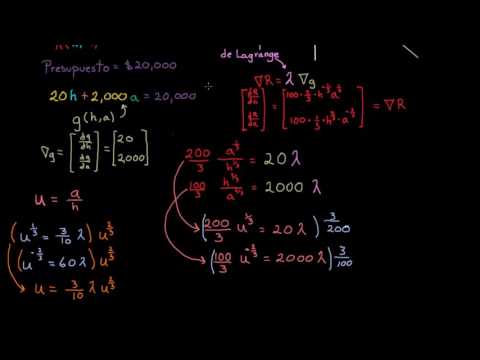Competencias de la lección

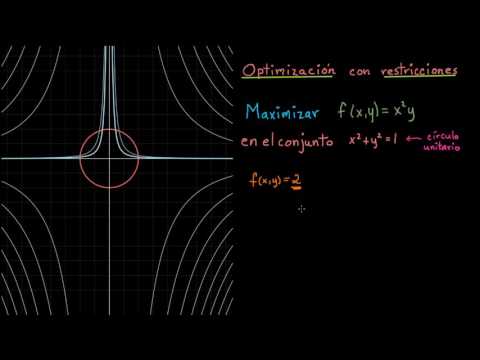
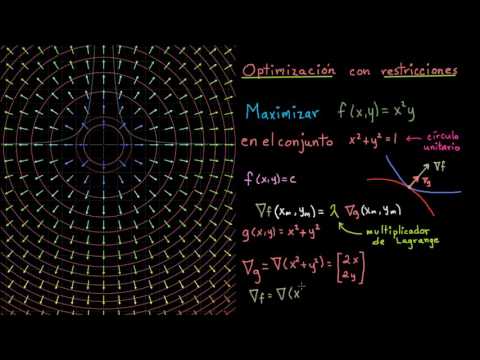
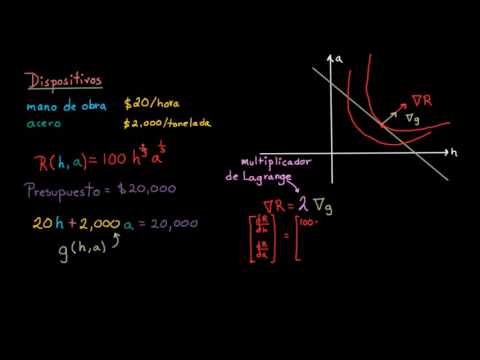
• Al finalizar la lección, el estudiante podrá utilizar los multiplicadores de Lagrange para encontrar los puntos óptimos (máximos o mínimos) de una función sujeta a una o más restricciones, comprendiendo el significado de las ecuaciones resultantes y cómo relacionan la función objetivo con las restricciones.
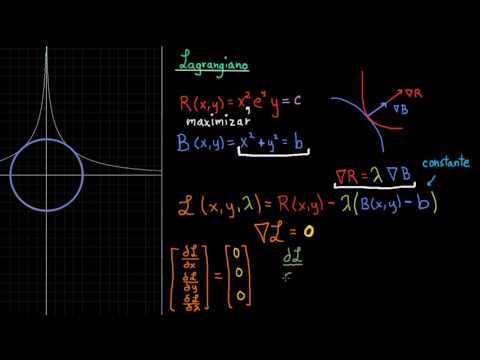
• Entender y explicar cómo el método de Lagrange implica que los gradientes de la función objetivo y de las restricciones sean paralelos en los puntos óptimos, lo que corresponde a la interpretación geométrica del problema.
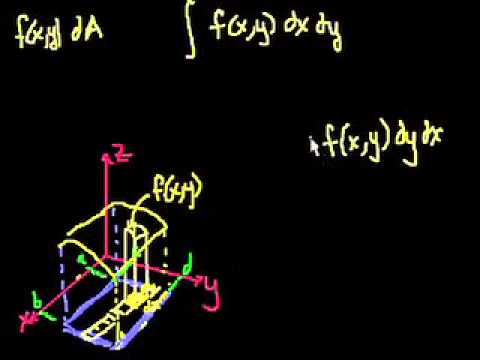
• Resolver integrales dobles sobre regiones rectangulares, utilizando correctamente los límites de integración y aplicando la técnica de integración iterada para calcular áreas, volúmenes o valores promedio de funciones sobre dichas regiones.
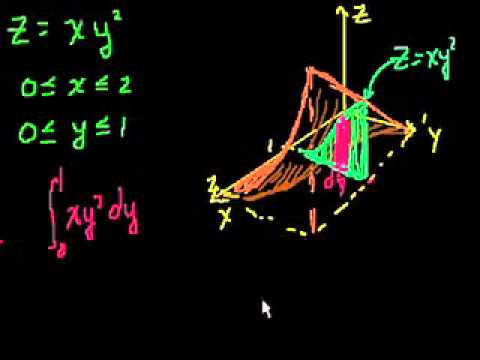
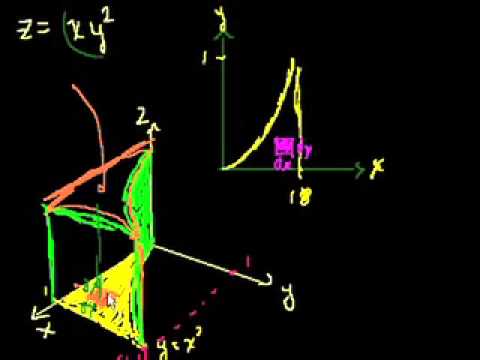
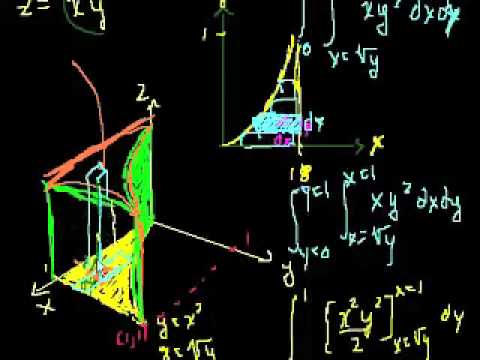
• Calcular integrales dobles sobre regiones generales (como regiones definidas por curvas), aplicando adecuadamente los límites de integración que dependen de las características de la región.
• Resolver problemas del mundo real que involucran el cálculo de cantidades físicas sobre regiones bidimensionales, como masas distribuidas, áreas de figuras complejas, y volúmenes bajo superficies.

Lección 1.2 Límites y continuidad de una función de varias variables. Derivadas parciales

1. (T2.3) Optimización restringida y multiplicadores de Lagrange:

   1. Máximos y mínimos con restricciones. (Bibliografía: Thomas p.845-848, Stewart p.976-977, Smith p.886-887).
   2. Multiplicadores de Lagrange. (Bibliografía: Thomas p.848-852, Stewart p.971-976, Smith p.887-893).

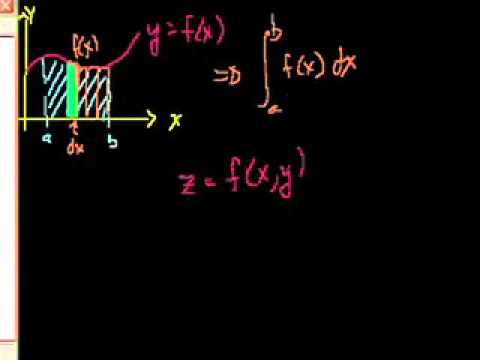
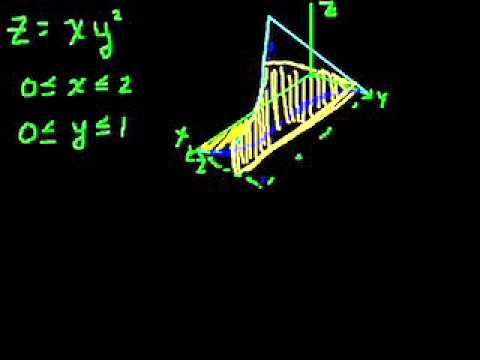
2. (T2.4) Integrales dobles sobre regiones rectangulares y regiones generales:

   1. Integrales dobles. (Bibliografía: Thomas p.870-872, Stewart p.988-992, Smith p.899-904).
   2. Integral iterada y teorema de Fubini. (Bibliografía: Thomas p.872-874, Stewart p.993-996, Smith p.905).