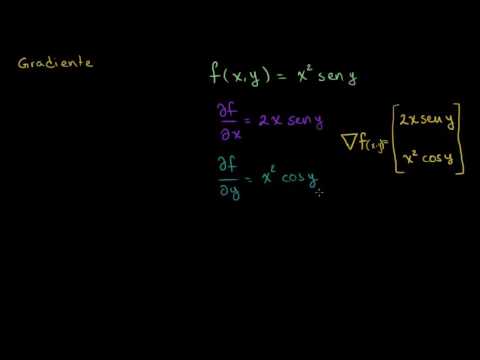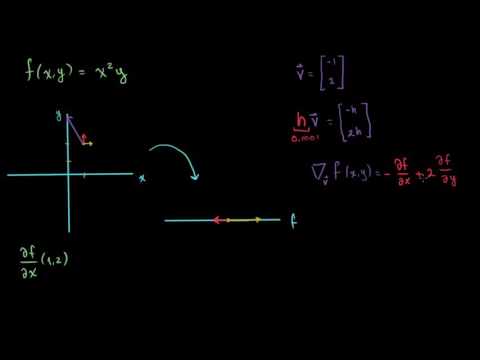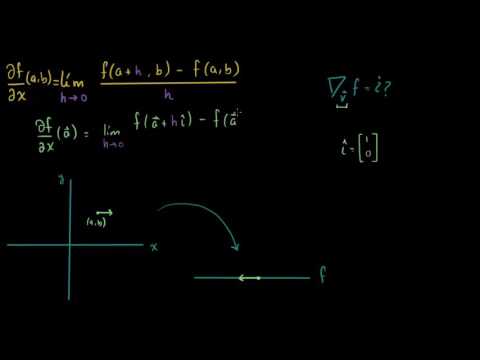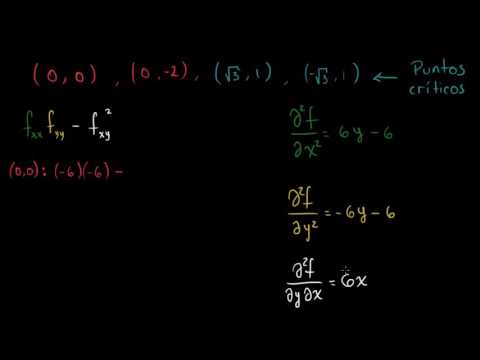Cálculo III
Escuela de Matemáticas
Facultad de Ciencias
Universidad Industrial de Santander
Módulo 2. Derivada de funciones.
Lección 2.1. Derivada direccional y valores extremos de una función de varias variables.
Volver al módulo
1. Preparación de la lección
Competencias de la lección
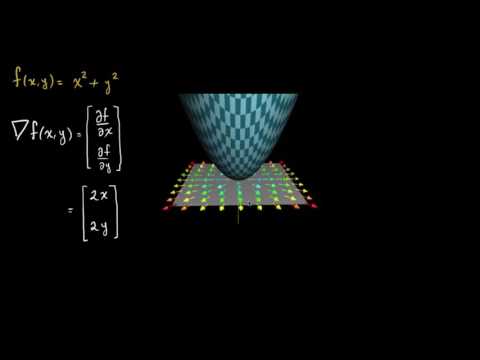
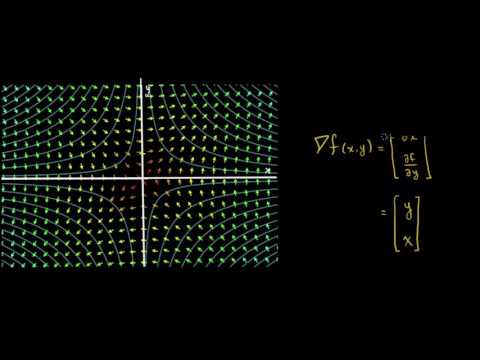
- Al finalizar la lección, el estudiante podrá calcular el gradiente de una función de varias variables y entender que el gradiente apunta en la dirección de mayor tasa de cambio de la función, interpretándolo como un vector que indica cómo se modifica la función en el espacio.
- Calcular la derivada direccional de una función en cualquier dirección, comprendiendo cómo la función cambia no solo en las direcciones de los ejes coordenados, sino en cualquier dirección arbitraria especificada por un vector.
- Interpretar el gradiente como una herramienta útil para determinar direcciones óptimas de cambio en contextos físicos, como campos de temperatura o velocidad, y utilizar la derivada direccional para evaluar cambios en direcciones específicas.
- Encontrar los puntos críticos de una función de varias variables, resolver el sistema de ecuaciones resultante de igualar el gradiente a cero, y determinar si esos puntos corresponden a máximos, mínimos o puntos de silla.
- Utilizar la matriz Hessiana para analizar los puntos críticos de una función y clasificar los valores extremos, determinando si los puntos son máximos, mínimos o puntos de silla en función de las segundas derivadas.
Catálogo de Videos
Catálogo de Simuladores
Catálogo de Libros
Cálculo de varias variables (Robert Smith)
Cálculo: Trascendentes tempranas (Stewart, James; Clegg, Daniel; Watson, Saleem)
Cálculo de varias variables. Trascendentes tempranas (Stewart, James; Clegg, Daniel; Watson, Saleem)
Cálculo de varias variables (James Stewart)
Cálculo varias variables (George B. Thomas)
Matemáticas III Cálculo de varias variables (Larson, Ron; Edwards, Bruce)
2. Profundización de la lección
L2.1 Derivada direccional y valores extremos de una función de varias variables.
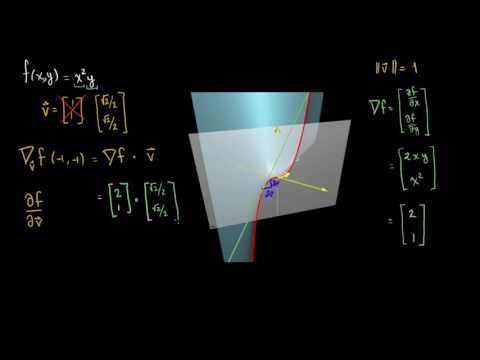
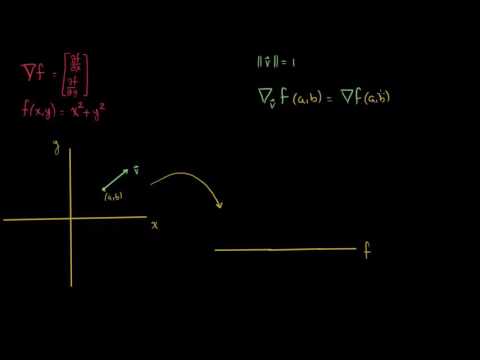
(T2.1) Gradiente y derivada direccional de una función de varias variables.
(T2.2) Valores extremos de una función de varias variables.
Gradiente y derivada direccional de una función de varias variables.
- Derivada direccional. (Bibliografía: Thomas p.818-820, Stewart p.946-949, Smith p.863-864).
- Gradiente. (Bibliografía: Thomas p.820-824, Stewart p.949-952, Smith p.864-866).
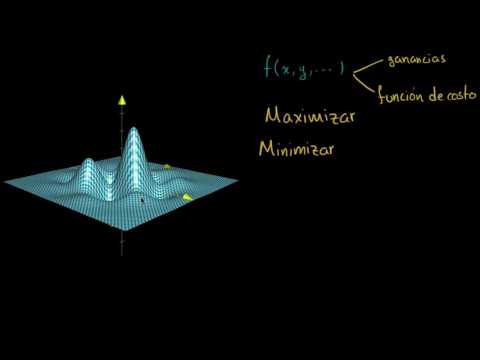
Valores extremos de una función de varias variables.
- Mínimos, máximos y puntos silla. (Bibliografía: Thomas p.836-842, Stewart p.959-962, Smith p.873-877).
3. Reto de la lección
Resumen
4. Cierre de la lección
Autoevaluación
¿Qué es el gradiente de una función de varias variables y cómo se interpreta geométricamente?
¿Qué es la derivada direccional y cómo se calcula usando el gradiente?
¿Cómo se determinan los puntos críticos de una función de varias variables?
¿Qué método se utiliza para clasificar los puntos críticos como máximos, mínimos o puntos de silla?
¿Cómo se relaciona el gradiente con los valores extremos de una función?